
台形の面積を、公式なしで求めてみましょう。
面積の定義は、次の通りでした。
1辺の長さが1の正方形の面積は「1」
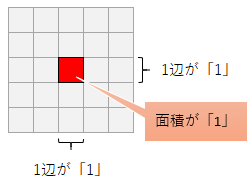
そして、三角形の面積は、次のように求められました。
| 三角形の面積 | = | 底辺 | × | 高さ | ÷ | 2 |
三角形の面積の求め方を使って、下の図の赤い部分の台形の面積を求められます。
台形も、平行四辺形と同じように、対角線を1本引き、2つの三角形に分けます。
片方の三角形に注目してみましょう。
次の図でオレンジ色の三角形の面積を考えます。
逆さまになっていますが、台形の1辺を三角形の底辺と考えると、台形の高さが三角形の高さになります。
三角形の面積は
| 底辺 | × | 高さ | ÷ | 2 |
で求められるので、底辺と高さの長さが同じであれば、どんな形の三角形でも面積は同じになります。
これをふまえて、オレンジ色の三角形の形を、次の図のように変えてみましょう。
底辺も高さも、形を変える前の三角形と同じ長さなので、この三角形も形を変える前の三角形と同じ面積になります。
さて、ここでよく見ると、台形が三角形に変わりました。
台形の一部の三角形を、面積を変えずに形を変えただけなので、できた大きな三角形(赤色)の面積は、もとの台形の面積と同じです。
つまり、台形の面積を求めるには、この赤い三角形の面積を求めればよいことになります。
この三角形の面積は
| (1+4) | × | 4 | ÷ | 2 | = | 10 |
| 上底+下底 | 高さ | 赤い三角形の面積 = 台形の面積 |
と求められ、これが台形の面積です。
ここから、台形の面積は、以下のように求められることがわかりました。
| 台形の面積 | = | (上底+下底) | × | 高さ | ÷ | 2 |