
平行四辺形の面積を、公式なしで求めてみましょう。
面積の定義は、次の通りでした。
1辺の長さが1の正方形の面積は「1」
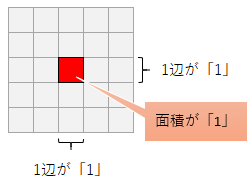
そして、三角形の面積は、次のように求められました。
| 三角形の面積 | = | 底辺 | × | 高さ | ÷ | 2 |
三角形の面積の求め方を使って、下の図の赤い部分の平行四辺形の面積を求められます。
平行四辺形は向かい合う辺が平行なので、下の図の青い部分の三角形は、同じ形・同じ大きさ、つまり合同な三角形になります。
三角形1つの底辺と高さは下の図のようになります。
そのため、三角形1つの面積は、
| 3 | × | 4 | ÷ | 2 | = | 6 |
| 底辺 | 高さ | 三角形1つの面積 |
と求められました。
今回求めたいものは平行四辺形です。
平行四辺形は、先ほど面積を求めた三角形2つ分の面積となるため、
| 3 | × | 4 | ÷ | 2 | × | 2 | = | 12 |
| 底辺 | 高さ | 三角形2つ分 | 平行四辺形の面積 |
と求めることができました。
「÷2×2」の部分では、2で割って2でかけているので、元の数に戻ります。
つまり、平行四辺形の面積を求めるには、「÷2×2」の部分は消してしまって、以下のように求められます。
| 平行四辺形の面積 | = | 底辺 | × | 高さ |
なお、平行四辺形の辺は長方形とはちがって